Oriented Bounding Boxes in VEX

Recently I undertook a Machine Learning course over at Coursera. The course covers a lot of the fundamental maths of Machine Learning and gives you an understanding that will allow you to go on and jump into things like TensorFlow with a greater depth of knowledge that you wouldn't otherwise have. If you're interested to find out more, here's the link:

https://www.coursera.org/learn/machine-learning

The reason I'm mentioning all of this here is that in week 8 of the course, the instructor covers Principal Component Analysis (PCA) which can be used to remove the number of data inputs to your training model. It does this by identifying which components of your data have a correlation to other components. For example, the number of bedrooms a house has will likely be correlated to the overall square footage of the house. Using PCA, you can reduce your data set down to the minimum inputs your training model needs in order to work efficiently. This can be massively helpful in reducing computational load when dealing with a large amount of data.

To put it simply, PCA basically just tells you in which directions the data varies the most. In Machine Learning, you can use those directions (which would be in N-parameter space, not just 3 dimensions) to rotate, reproject, and remove redundant data.

It turns out that the mathematical methods involved are exactly what you would need to calculate the axis directions of an oriented bounding box for a cloud of points in 3D.

As I'm sure you already know, this can be an incredibly useful thing to do in a number of situations in CG. For example, using as a simplified collision hull in simulations. In Houdini, the Bound SOP will already do this for you, but I've found this to be an interesting exercise to understand how to calculate this myself.

Overview

So what are we trying to solve? The problem is, given some geometry that's rotated at some arbitrary angle, how do we calculate an oriented bounding box so that it fits in the most intuitive way?

The image below shows Houdini's test Squab geometry and the bounding box that we're trying to calculate in white. We can see that it fits the geometry well and aligns in a way that we would expect:

Steps To Solve

These are the steps that we need to go through to calculate the oriented bounding box of a set of points:

1. Calculate the centre or average (mean) position of the points. Houdini handily gives us a function to do this in the getbbox_center() VEX function.

2. Build the Covariance Matrix.

3. Process the Covariance Matrix using Singular Value Decomposition (SVD). More on this later.

4. Use the output of SVD to find the principal axes of the oriented bounding box.

5. Find the projection of the points along each of the axes (equivalent to transforming into local space of the found axes orientation) and calculate the min/max of each component to find the bounding box size.

All sounds a bit complicated, right? And those Wikipedia pages look a bit intimidating with all that notation. But don't worry! For our purposes, we can keep it quite simple, and I'll walk you through the steps.

Don't forget... those Wikipedia pages have been written by mathematicians, to be read by other mathematicians. I don't think anyone would consider them "easy reading", and they assume a level of knowledge that most people won't have if they're coming to this for the first time.

Let's deal with this step by step. We'll be using VEX to do this in an Attribute Wrangle SOP with it set to process in Detail mode, so the code will be processed in a single thread rather than trying to run it multi-threaded. You can follow along with each step below, or just skip to the bottom and grab the full VEX listing.

There's no reason you can't follow these similar steps in a Python SOP using NumPy but you'll find it significantly slower as it takes a significant amount of time to populate a NumPy array from the geometry's point positions.

So let's start with the first step.

Step 1: Find The Center Of The Points

As already mentioned above, this is the easy bit. We can just do this:

vector c = getbbox_center(1);

I don't usually use single characters for variable names (honest!), but in this case, it makes things a little simpler to write.

You'll notice that I'm pulling the geometry from input index 1, which is the second input of the Wrangle SOP. That's because I only want to output the bounding box geometry that I'm creating in the Wrangle. I don't want to merge it with the input geometry that I'm processing.

I should point out that the bounding box that this function is referring to is not the oriented bounding box that ultimately we're after, but the axis-aligned bounding box. Since we're in SOPs, that's technically in Houdini's Object Space, but to avoid confusion let's just assume that's the same as World Space. I.e. that our top-level Geometry Object in Houdini doesn't have any rotation.

If we want to calculate this for ourselves in VEX instead of using getbbox_center(), we would just add all the point positions together and divide by the number of points. I.e.

vector c = {0,0,0};
int numpts = npoints(1)
for( int i = 0 ; i < numpts ; i++) {
    c += point(1, "P", i);
}
c /= numpts;

So why do we need the centre of the points? Well, the formula to compute the Covariance Matrix (in the next step) requires the average value on each axis of all the positions. This is basically just a fancier way of saying we need the central or average position. More on that in a minute.

Step 2: Build The Covariance Matrix

"Okay", I hear you say, "but what the f*** is a covariance matrix!?".

Good question!

The simplest way to think about a covariance matrix is that it describes how data varies compared to other data. In our case, with 3D points, it describes how each point position's coordinate axis is, on average, related to the other coordinate axes.

We'll take this step by step. If it helps you, you can skip to the code implementation of this below but it's a good skill to try to develop your understanding of how to read the maths notation, so come back after and see if you can get your head around it.

Let's start tackling this by looking at Wikipedia's definition of the covariance matrix. Go have a look and see if you can make sense of it before reading on.

Yes, it's ugly! But it's actually easier to understand than one might first think. Let's break it down.

The first expression where it defines X, in our case, that's just referring to the point position, where n=3, so that X1, X2, and X3 are actually just our x, y, and z coordinates for our points. So instead of going up to n, we're only going up to 3 dimensions in our data.

What's with the "T" on the end? All that means is that it's treating that list of numbers as a column vector. I.e. rotating its appearance so that instead of (x, y, z), it's actually:

This doesn't really matter too much. Vectors can be represented either way. It only really matters to be specific when multiplying with other vectors or matrices.

The next paragraph:

This is saying we have a 2 dimensional matrix K. In our case, it's a 3x3 matrix because the i and j are looping over the x, y, and z axes in each direction.

This is made a bit more obvious when you look at the following line:

Initially, looking at this, it's hard to get your head around how this relates to a list of points in 3D. How would this equation deal with running over a list of thousands of points in a mesh? The next line helps with understanding though:

So the looping over our list of points happens within the mean operation E. Let's break it down a bit further to help with understanding.

What does this mean?

This is just the mean (or average) over all the points of the ith axis. So which axis is that? For the first column of our K matrix, i indicates the x axis. For the second column, i indicates the y axis, and z for the third.

What about this then?

The j subscript is again looping over an axis, but this time, it's changing with our K matrix's row.

So let's rewrite the equation to be something a bit more readable. The first simplification is that we'll write it to show the value of a single value in our 3x3 matrix. In this case, it's the equation specifically for calculating the value that specifies the relation between the x and y axes.

We'll replace the Xs with the coordinate axes, and the E with something a bit more familiar (at least to me) which is to use the bar notation to indicate the average. This time, we're using x and y to indicate the x and y axes, and i now refers to the point number (not the same i as above which was talking about which coordinate axis).

I've also written "avg" to indicate we're taking an average over the whole thing. It helps with understanding that the value of this equation is just a single number. Hopefully, that looks a bit clearer to you.

The subscript xy of K just denotes which axes we're using inside the expression on the right-hand side. So if the subscript was zy instead, then we would be doing calculations using z and y instead of x and y.

Alternatively, we could write it like this, using the sigma notation to replace the "avg" where n is the number of points we're averaging over:

Whatever you prefer.

The covariance matrix then looks like this:

Just replace the x and y in our equation above, with the appropriate axis being used as suffixes for K and calculate each element.

If you've still not quite wrapped your head around it, don't worry, let's look at some VEX code that will compute this.

Note that we're using input 1 (not 0) to pull in the geometry so that the VEX Wrangle starts with empty geometry, rather than the geometry of the mesh that we're analysing.

vector c = getbbox_center(1);
matrix3 @cov_mat;
int numpts = npoints(1);

for(int i=0;i<numpts;i++)
{
    vector p = point(1, "P", i);
    @cov_mat.xx += (p.x-c.x)*(p.x-c.x);
    @cov_mat.xy += (p.x-c.x)*(p.y-c.y);
    @cov_mat.xz += (p.x-c.x)*(p.z-c.z);   
 
    @cov_mat.yx += (p.y-c.y)*(p.x-c.x);
    @cov_mat.yy += (p.y-c.y)*(p.y-c.y);
    @cov_mat.yz += (p.y-c.y)*(p.z-c.z); 
 
    @cov_mat.zx += (p.z-c.z)*(p.x-c.x);
    @cov_mat.zy += (p.z-c.z)*(p.y-c.y);
    @cov_mat.zz += (p.z-c.z)*(p.z-c.z);   
}
@cov_mat/=float(numpts);

If you know about outer products, then you might have already spotted that the above code is equivalent to this:

vector c = getbbox_center(1);
matrix3 @cov_mat;
int numpts = npoints(1);

for(int i=0;i<numpts;i++)
{
    vector p = point(1, "P", i) - c;
    @cov_mat += outerproduct(p, p);
}
@cov_mat/=float(numpts);

If you've not encountered the outer product before, then for two 3 component vectors, the outer product is:

The outer product is basically just treating two vectors like a column and row matrix and then multiplying them together.

I've not run any profiling on this, but I would imagine that it's faster to use the built-in VEX function, rather than calculating each of the individual matrix elements manually.

Understanding the Covariance Matrix

Before we talk about Singular Value Decomposition (SVD), let's build up some intuition about what the covariance matrix is all about.

We can think of the covariance matrix as a 3x3 transform that transforms a sphere into an ellipsoid. Visually, the ellipsoid appears to be aligned to the direction of the greatest variance of the points, and the dimensions are an indication of the greatest variation.

For example, take a simple polygon box oriented at a random rotation:

If we find the 3x3 covariance matrix of these points, and then transform a sphere with it, the sphere will look like this:

That seems very close to what we want right? Almost, yes, but not quite. The issue is that the covariance matrix isn't a pure rotation and scale, there's also skew involved. If we try putting in geometry along the x, y, and z axes, we can see this skewing clearly.

Okay, so now what? How do we get some axes aligned in a way that makes sense intuitively? That's where Singular Value Decomposition (SVD) comes in.

Step 3: Singular Value Decomposition (SVD)

Singular Value Decomposition lets us break down certain matrices ( like the covariance matrix) into three matrices that represent two rotations and a scale. These three matrices can be multiplied in order to give the original, like this:

Again, the "T" just means transpose. There are other complexities to SVD we're going to ignore regarding imaginary solutions, but they're safe to ignore in our situation.

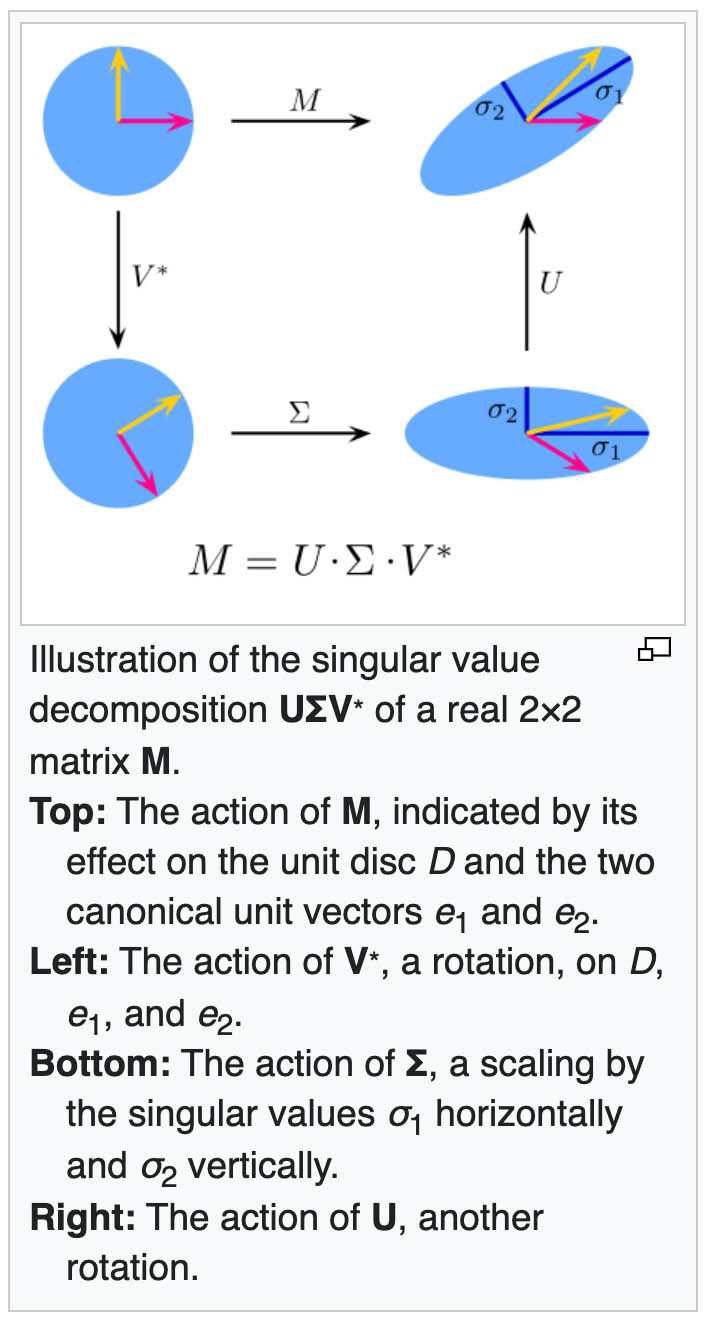
As the diagram (right) on the Wikipedia page shows, we can think of these three matrices as doing a rotation, followed by a scale, followed up by a final rotation.

The V matrix deals with the initial rotation of the axes,

The 𝚺 (Sigma) matrix deals with scaling.

Finally, the U matrix handles the rotational alignment.

The M matrix mentioned on the right is the combined operation of all three matrices. In this article, M would be the covariance matrix.

Looking at this, it would appear (correctly) that the U matrix is what we're after.

So the question now is, how do we do SVD in VEX? Well, it's actually super easy because, since version 18.0, Houdini gives us a VEX equation called svddecomp() to do it. It has three outputs, and so we call it like this:

matrix3 out_u;
vector out_s;
matrix3 out_v;

svddecomp(@cov_mat, out_u, out_s, out_v);

Note that when doing SVD, the Sigma matrix is a diagonal matrix as it represents pure scale, and so instead of returning a full matrix, Houdini just returns a vector containing those diagonal values instead.

Another thing to note is that this is not a general SVD function that works on any size of matrix. This function only operates on 3x3 matrices, but for our purposes that's fine.

Step 4: Find The Principal Axes Of The Oriented Bounding Box

If you run the SVD function and pass it the covariance matrix, the "out_u" matrix will contain the x, y, and z axes in its columns. The simplest way to extract the principal axes easily with VEX, is to transpose the matrix and then use the set() function to turn the 3x3 matrix into an array of vector3, like this:

vector vec[];
vec = set(transpose(out_u));

Great, we now have our principal axes for our point cloud in a vector array. That's all the hardest maths done.

The final step is relatively trivial. We just need to calculate the bounds of our data along the principal axes and create our bounding box.

Step 5: Making The Bounding Box

There are different approaches to constructing your bounding box in Houdini, depending on what you're wanting to do.

You could either:

1. Calculate the points at each corner and connect them with edges or quad faces

2. Make a single point and set the appropriate attributes so that doing a "copy to points" operation in Houdini with a cube of size 1 will give you the correct result.

Here we'll take the first approach, but whatever you decide, we will still need to calculate the actual size of the bounding box. At the moment, we only have the 3 axes showing the principal axes of the point data.

The steps to calculating the bounds of the points along the 3 principal axes are as follows:

1. Calculate a rotation matrix using the three axes we got from doing SVD.

2. Invert the rotation matrix

3. For each point, subtract the center position and rotate it using the inverted rotation matrix. This aligns the input points with the world axes.

4. Calculate the max and min boundaries of the transformed points.

So first step, we can just use Houdini's maketransform() function and pass it the z and y vectors from the last section.

matrix3 mat = maketransform(@vec[2], @vec[1]);

Next, we invert the matrix using Houdini's invert() function:

matrix3 inv_mat = invert(mat);

Then we need to initialise a couple of detail vector attributes to store the bounding box.

We assign the maximum float value possible to the components of @bbmin, and the minimum value possible to the components of @bbmax. This is just to ensure that the first point position in the loop below initialises both these values straight away without having to use an if statement to do so on the first iteration of the loop.

vector @bbmin = {1.0e38, 1.0e38, 1.0e38};
vector @bbmax = {-1.0e38, -1.0e38, -1.0e38};

Finally, we loop through the points. Each point has the average point position subtracted, and then rotated back, where we measure the bounding box.

for(int i=0;i<numpts;i++)
{
    vector p = point(1, "P", i) - c;
    vector rot_p = inv_mat * p;
    @bbmin = min(rot_p, @bbmin);
    @bbmax = max(rot_p, @bbmax);    
}

Note that @bbmin is usually not equal and opposite (in sign) to @bbmax. The asymmetry between these two values is just down to how evenly the points are distributed over the geometry.

If you are taking the second approach for making a bounding box (i.e. a single point with attributes), then you will need to correct this asymmetry by modifying the center position c and adjusting the bounds accordingly.

To make the bounding box geometry; first, we calculate each corner position (in world position) and put it in an array of vectors:

vector p[] = array(set(@bbmin[0], @bbmin[1], @bbmin[2]), 
    set(@bbmax[0], @bbmin[1], @bbmin[2]), 
    set(@bbmin[0], @bbmax[1], @bbmin[2]), 
    set(@bbmax[0], @bbmax[1], @bbmin[2]), 
    set(@bbmin[0], @bbmin[1], @bbmax[2]), 
    set(@bbmax[0], @bbmin[1], @bbmax[2]), 
    set(@bbmin[0], @bbmax[1], @bbmax[2]),
    set(@bbmax[0], @bbmax[1], @bbmax[2]));

Next. we transform each corner of the bounding box using the matrix mat that we created earlier.

for(int i=0;i<8;i++)
{
    p[i] = c + mat * p[i];
}

VEX allows us to make our own functions, so we'll write one to make a line segment between two vectors:

void add_line(vector p1; vector p2)
{
    int pt1 = addpoint(geoself(), p1);
    int pt2 = addpoint(geoself(), p2);    
    int prim = addprim(geoself(), "polyline");
    addvertex(geoself(), prim, pt1);
    addvertex(geoself(), prim, pt2);    
}

and now we can add the lines along each edge of the bounding box:

add_line(p[0], p[1]);
add_line(p[2], p[3]);
add_line(p[3], p[1]);
add_line(p[0], p[2]);

add_line(p[4], p[5]);
add_line(p[6], p[7]);
add_line(p[7], p[5]);
add_line(p[4], p[6]);

add_line(p[0], p[4]);
add_line(p[1], p[5]);
add_line(p[2], p[6]);
add_line(p[3], p[7]);

Final Result

To show it in action; below you'll see that I'm using the Squab test geometry that comes with Houdini, and transforming it before feeding it into the second input of the wrangle node (set to Detail mode):

The VEX is fast to compute, so you can transform the geometry and see the bounding box update in real-time.

Code Listing:

To use:

• Create an Attribute Wrangle SOP set to "Detail" mode.

• Feed your geometry into the second input. (This means that the output of the wrangle node is just the bounding box, and not the input geometry as well.)

• Copy and paste the code below into it.

// Get the center of the rotated geometry
vector c = getbbox_center(1);

matrix3 @cov_mat;
int numpts = npoints(1);

// The quick way to construct the covariance 
// matrix using outerproduct()
for(int i=0;i<numpts;i++)
{
    vector p = point(1, "P", i) - c;
    @cov_mat += outerproduct(p, p);
}
@cov_mat/=float(numpts);

// Perform Singular Value Decomposition(SVD)
matrix3 @out_u;
vector out_s;
matrix3 out_v;
svddecomp(@cov_mat, @out_u, out_s, out_v);

// Get the 3 principal axes from the result of SVD.
vector @vec[];
@vec = set(transpose(@out_u));

// Make rotation matrix out of the principal axes
matrix3 mat = maketransform(@vec[2], @vec[1]);

// Make an inverse matrix so that we can rotate the points
// from the rotated frame, back to the world aligned frame.
matrix3 inv_mat = invert(mat);

// Calculate the bounding box min/max for 
// the points in world space
vector @bbmin = {1.0e38, 1.0e38, 1.0e38};
vector @bbmax = {-1.0e38, -1.0e38, -1.0e38};

for(int i=0;i<numpts;i++)
{
    vector p = point(1, "P", i) - c;
    vector rot_p = inv_mat * p;
    @bbmin = min(rot_p, @bbmin);
    @bbmax = max(rot_p, @bbmax);    
}

// Make a bounding box in world space using the
// min/max values we just found
vector p[] = array(set(@bbmin[0], @bbmin[1], @bbmin[2]), 
    set(@bbmax[0], @bbmin[1], @bbmin[2]), 
    set(@bbmin[0], @bbmax[1], @bbmin[2]), 
    set(@bbmax[0], @bbmax[1], @bbmin[2]), 
    set(@bbmin[0], @bbmin[1], @bbmax[2]), 
    set(@bbmax[0], @bbmin[1], @bbmax[2]), 
    set(@bbmin[0], @bbmax[1], @bbmax[2]),
    set(@bbmax[0], @bbmax[1], @bbmax[2]));

// Transform the bounding box into the rotated frame
for(int i=0;i<8;i++)
{
    p[i] = c + mat * p[i];
}

// Helper function to add a line segment
void add_line(vector p1; vector p2)
{
    int pt1 = addpoint(geoself(), p1);
    int pt2 = addpoint(geoself(), p2);    
    int prim = addprim(geoself(), "polyline");
    addvertex(geoself(), prim, pt1);
    addvertex(geoself(), prim, pt2);    
}

// Add line segments for the rotated bounding box
add_line(p[0], p[1]);
add_line(p[2], p[3]);
add_line(p[3], p[1]);
add_line(p[0], p[2]);

add_line(p[4], p[5]);
add_line(p[6], p[7]);
add_line(p[7], p[5]);
add_line(p[4], p[6]);

add_line(p[0], p[4]);
add_line(p[1], p[5]);
add_line(p[2], p[6]);
add_line(p[3], p[7]);